1220.00 Indigs

1220.10 Definition

Definition: All numbers have their own integrity.

1220.11

The name digit comes from finger. A finger is a digit. There are five fingers on each hand. Two sets of five digits give humans a propensity for counting in increments of 10.

1220.12

Curiosity and practical necessity have brought humans to deal with numbers larger than any familiar quantity immediately available with which to make matching comparison. This frequent occurrence induced brain-plus-mind capabilities to inaugurate ingenious human information-apprehending mathematical stratagems in pure principle. If you are looking at all the pebbles on the beach or all the grains of sand, you have no spontaneous way of immediately quantifying such an experience with discrete number magnitude. Quantitative comprehension requires an integrative strategy with which to reduce methodically large unknown numbers to known numbers by use of obviously well- known and spontaneously employed linear-, area-, volume-, and time-measuring tools.

1220.13 Indig Table A: Comparative Table of Modular Congruences of Cardinal Numbers

Indig Table A: Comparative Table of Modular Congruences of Cardinal Numbers: This is a comparative table of the modular congruences of cardinal- number systems as expressed in Arabic numerals with the individual integer symbols integrated as indigs, which discloses synergetic wave-module behaviors inherent in nature’s a priori, orderly, integrative effects of progressive powers of interactions of number:

Visually	Nonintegrated	Indigs	Indig
1	1	1
11	11	2
1 1 1	111	3
11 11	1111	4
11 1 11	11111	5
111 111	111111	6
111 1 111	1111111	7
11 11 11 11	11111111	8
111 111 111	111111111	9
two hands	1111111111	10	1
too much	11111111111	11	2

1220.14

Man started counting large numbers which he did not recognize as a discrete and frequently experienced pattern by modularly rhythmic repetitive measuring, or matching, with discrete patterns which he did recognize__as, for instance, by matching the items to be counted one for one with the successive fingers of his two hands. This gave him the number of separate items being considered. Heel-to-toe stepping off of the number; or foot-after-foot length dimensions; or progressively and methodically covering areas with square woven floor mats of standard sizes, as the Japanese tatami and tsubo; or by successive mouthfuls or handfuls or bowls full, counted on the fingers of his hands, then in multiples of hands (i.e., multiples of ten), gave him commonly satisfactory volume measurements.

1220.15

Most readily humans recognized and trusted one and one making two, or one and two making three, or two and two making four. But an unbounded loose set of 10 irregular and dissimilar somethings was not recognizable by numbers in one glance: it was a lot. Nor are five loose, irregular, and dissimilar somethings recognizable in one glance as a number: they are a bunch. But a human hand is boundaried and finitely recognizable at a single glance as a hand, but not as a discrete number except by repetitively acquired confirmation and reflexive conditioning. Five is more recognizable as four fingers and a thumb, or even more readily recognizable as two end fingers (the little and the index), two fingers in the middle, and the thumb (2 + 2 + 1 = 5).

1220.16

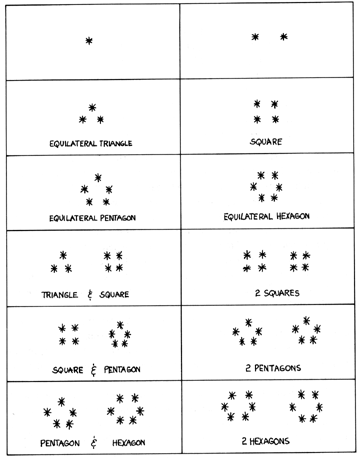
Symmetrical arrays of identically shaped and sized, integrally symmetric objects evoke spontaneous number identification from one to six, but not beyond. Paired sets of identities to six are also spontaneously recognized; hence we have dice and dominoes.

1220.17

Thus humans learned that collections of very large numbers consist of multiples of recognizable numbers, which recognition always goes back sensorially to spontaneously and frequently proven matching correspondence with experientially integrated pattern simplexes. One orange is a point (of focus). Two oranges define a line. Three oranges define an area (a triangle). And four oranges, the fourth nested atop the triangled first three, define a multidimensional volume, a tetrahedron, a scoop, a cup.1 (Footnote 1: This may have been the genesis of the cube__ where all the trouble began. Why? Because man’s tetrahedron scoop would not stand on its point, spilled, frustrated counting, and wasted valuable substances. So humans devised the square-based volume: the cube, which itself became an allspace-filling multiple cube building block easily appraised by “cubing” arithmetic.)

1220.20 Numerological Correspondence

Numerological Correspondence: Numerologists do not pretend to be scientific. They are just fascinated with a game of correspondence of their “key” digits - finger counts, ergo, 10 digits - with various happenstances of existence. They have great fun identifying the number “seven” or the number “two” types of people with their own ingeniously classified types of humans and types of events, and thereafter imaginatively developing significant insights which from time to time seem justified by subsequent coincidences with reality. What intrigues them is that the numbers themselves are integratable in a methodically reliable way which, though quite mysterious, gives them faithfully predictable results. They feel intuitively confident and powerful because they know vaguely that scientists also have found number integrity exactly manifest in physical laws.

1220.21

The numerologists have also assigned serial numbers to the letters of the alphabet: A is one, B is two, C is three, etc. Because there are many different alphabets of different languages consisting of various quantities of letters, the number assignments would not correspond to the same interpretations in different languages. Numerologists, however, preoccupied only in their single language, wishfully assumed that they could identify characteristics of people by the residual digits corresponding to all the letters in the individual’s complete set of names, somewhat as astrologists identify people by the correspondences of their birth dates with the creative picturing constellations of the Milky Way zoo = Zodiac = Celestial Circus of Animals.

1221.00 Integration of Digits

1221.10 Quantifying by Integration

Early in my life, I became interested in the mathematical potentials latent in the methodology of the numerologists. I found myself increasingly intrigued and continually experimenting with digit integrations. What the numerologist does is to add numbers as expressed horizontally; for instance: 120 = 1 + 2 + 0 = 3 Or: 32986513 = 3+2+9+8+6+5+1+3 = 37 = 3+7 = 10 = 1+0 = 1, Numerologically, 32986513= 1 Or: 59865279171 = 5+9 = 14+8 = 22+6 = 28+5 = 33+2 = 35+7 = 42+9 = 51+1 = 52+7 = 59+1 = 60 = 6+0 = 6, Numerologically, 59865279171 = 6.

1221.11

Though I was familiar with the methods of the calculus__for instance, quantifying large, irregularly bound areas__explorations in numerology had persuaded me that large numbers themselves, because of the unique intrinsic properties of individual numbers, might be logically integratable to disclose initial simplexes of sensorial interpatterning apprehendibility.

1221.12

Integrating the symbols of the modular increments of counting, in the above case in increments of 10, as expressed in the ten-columnar arrays of progressive residues (less than ten — or less than whatever the module employed may be), until all the columns’ separate residues are reduced to one integral digit, i.e., an integer that is the ultimate of the numbers that have been integrated. Unity is plural and at minimum two. (See Secs. 240.03; 527.52; and 707.01.)

1221.13

As a measure of communications economy, I soon nicknamed as indigs the final unitary reduction of the integrated digits. I use indig rather than integer to remind us of the process by which ancient mathematicians counting with their fingers (digits) may have come in due course to evolve the term integer.

1221.14

I next undertook the indigging of all the successive modular congruence systems ranging from one-by-one, two-by-two pairs to “by the dozens,” i.e., from zero through 12. (See modulo-congruence tables, Sec. 1221.20.)

1221.15

The modulo-congruence tables are expressed in both decimal and indig terms. In each of the 13 tables of the chart, the little superscripts are the indigs of their adjacently below, decimally expressed, corresponding integers.

1221.16

The number of separate columns of the systematically displayed tables corresponds with the modulo-congruence system employed. Inspection of successive horizontal lines discloses the orderly indig amplifying or diminishing effects produced upon arithmetical integer progression. The result is startling.

1221.17

Looking at the chart, we see that when we integrate digits, certain integers invariably produce discretely amplifying or diminishing alterative effects upon other integers. One produces a plus oneness; Two produces a plus twoness; Three produces a plus threeness; Four produces a plus fourness. Whereafter we reverse, Five produces a minus fourness; Six produces a minus threeness; Seven produces a minus twoness; Eight produces a minus oneness. Nine produces zero plusness or minusness. One and ten are the same. Ten indigs (indig = verb intransitive) as a one and produces the same alterative effects as does one. Eleven indigs as two and produces the same alterative effects as a two. All the other whole numbers of any size indig to 1, 2, 3, 4, S, 6, 7, 8, or 9 — ergo, have the plus or minus oneness to fourness or zeroness alterative effects on all other integers.

1221.18

Since the Arabic numerals have been employed by the Western world almost exclusively as congruence in modulo ten, and the whole world’s scientific, political, and economic bodies have adopted the metric system, and the notation emulating the abacus operation arbitrarily adds an additional symbol column unilaterally (to the left) for each power of ten attained by a given operation, it is reasonable to integrate the separate integers into one integer for each multisymboled number. Thus 12, which consists of 1 + 2, = 3; and speaking numerologically, 3925867 = 4.

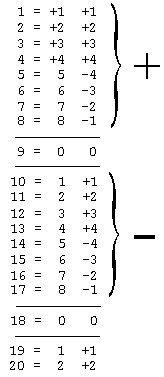
This provides an octave number system of a plus and minus octave and an (outside-out) and an (indise-out) differentiation, for every system has insideness (concave) and outsideness (convex) as well as two polar hemisystems.

1221.20 Indig Table B: Modulo-Congruence Tables

The effects of integers: One is + 1. Two is + 2. Three is + 3. Four is +4. Five is - 4. Six is - 3. Seven is - 2. Eight is -1. Nine is zero; nine is none. (The superior figures in the Table are the Indigs.)

Congruence in Modulo Zero Integrates to Gain or Lose 0:

	0
0 (Like nine)

Congruence in Modulo One Integrates to Gain 1:
(Each row gains 1 in each column)

	+1
1¹
2²
3³
4⁴
5⁵
6⁶
7⁷
8⁸
9⁹
10¹
11²
12³

Congruence in Modulo Two Integrates to Gain 2:
(Each row gains 2 in each column)

		+2
1¹	2²
3³	4⁴
5⁵	6⁶
7⁷	8⁸
9⁹	10¹
11²	12³
13⁴	14⁵
15⁶	16⁷

Congruence in Modulo Two Integrates to Gain 3:
(Each row gains 3 in each column)

			+3
1¹	2²	3³
4⁴	5⁵	6⁶
7⁷	8⁸	9⁹
10¹	11²	12³
13⁴	14⁵	15⁶
16⁷	17⁸	18⁹
19¹	20²	21³

Congruence in Modulo Four Integrates to Gain 4:
(Each row gains 4 in each column)

				+4
1¹	2²	3³	4⁴
5⁵	6⁶	7⁷	8⁸
9⁹	10¹	11²	12³
13⁴	14⁵	15⁶	16⁷
17⁸	18⁹	19¹	20²
21³	22⁴	23⁵	24⁶

Congruence in Modulo Five Integrates to Lose 4:
(Each row loses 4 in each column)

					-4
1¹	2²	3³	4⁴	5⁵
6⁶	7⁷	8⁸	9⁹	10¹
11²	12³	13⁴	14⁵	15⁶
16⁷	17⁸	18⁹	19¹	20²
21³	22⁴	23⁵	24⁶	25⁷
26⁸	27⁹	28¹	29²	30³

Congruence in Modulo Six Integrates to Lose 3:
(Each row loses 3 in each column)

						-3
1¹	2²	3³	4⁴	5⁵	6⁶
7⁷	8⁸	9⁹	10¹	11²	12³
13⁴	14⁵	15⁶	16⁷	17⁸	18⁹
19¹	20²	21³	22⁴	23⁵	24⁶
25⁷	26⁸	27⁹	28¹	29²	30³

Congruence in Modulo Seven Integrates to Lose 2:
(Each row loses 2 in each column)

							-2
1¹	2²	3³	4⁴	5⁵	6⁶	7⁷
8⁸	9⁹	10¹	11²	12³	13⁴	14⁵
15⁶	16⁷	17⁸	18⁹	19¹	20²	21³
22⁴	23⁵	24⁶	25⁷	26⁸	27⁹	28¹

Congruence in Modulo Eight Integrates to Lose 1:
(Each row loses 1 in each column)

								-1
1¹	2²	3³	4⁴	5⁵	6⁶	7⁷	8⁸
9⁹	10¹	11²	12³	13⁴	14⁵	15⁶	16⁷
17⁸	18⁹	19¹	20²	21³	22⁴	23⁵	24⁶
25⁷	26⁸	27⁹	28¹	29²	30³	31⁴	32⁵

Congruence in Modulo Nine Integrates to No Lose or Gain:
(Each row remains same value in its column)

									0
1¹	2²	3³	4⁴	5⁵	6⁶	7⁷	8⁸	9⁹
10¹	11²	12³	13⁴	14⁵	15⁶	16⁷	17⁸	18⁹
19¹	20²	21³	22⁴	23⁵	24⁶	25⁷	26⁸	27⁹
28¹	29²	30³	31⁴	32⁵	33⁶	34⁷	35⁸	36⁹

Congruence in Modulo Ten Integrates to Gain 1:
(Each row gains 1 in each column)

										+1
1¹	2²	3³	4⁴	5⁵	6⁶	7⁷	8⁸	9⁹	10¹
11²	12³	13⁴	14⁵	15⁶	16⁷	17⁸	18⁹	19¹	20²
21³	22⁴	23⁵	24⁶	25⁷	26⁸	27⁹	28¹	29²	30³
31⁴	32⁵	33⁶	34⁷	35⁸	36⁹	37¹	38²	39³	40⁴

Congruence in Modulo Eleven Integrates to Gain 2:
(Each row gains 2 in each column)

											+2
1¹	2²	3³	4⁴	5⁵	6⁶	7⁷	8⁸	9⁹	10¹	11²
12³	13⁴	14⁵	15⁶	16⁷	17⁸	18⁹	19¹	20²	21³	22⁴
23⁵	24⁶	25⁷	26⁸	27⁹	28¹	29²	30³	31⁴	32⁵	33⁶
34⁷	35⁸	36⁹	37¹	38²	39³	40⁴	41⁵	42⁶	43⁷	44⁸

Congruence in Modulo Twelve Integrates to Gain 3:
(Each row gains 3 in each column)

												+3
1¹	2²	3³	4⁴	5⁵	6⁶	7⁷	8⁸	9⁹	10¹	11²	12³
13⁴	14⁵	15⁶	16⁷	17⁸	18⁹	19¹	20²	21³	22⁴	23⁵	24⁶
25⁷	26⁸	27⁹	28¹	29²	30³	31⁴	32⁵	33⁶	34⁷	35⁸	36⁹
37¹	38²	39³	40⁴	41⁵	42⁶	43⁷	44⁸	45⁹	46¹	47²	48³

1222.00 Absolute Four and Octave Wave

1222.10 Prime Dichotomy

It is found that all decimally expressed whole numbers integrate into only nine digits. Looking at the charts (Indig Table B), we see the nine indigs resultant to the decimal system, or congruence in modulo ten, have integrated further to disclose only nine unique operational effects upon all other integers. These nine interoperational effects in turn reduce into only eight other integer-magnitude-altering effects and one no-magnitude-altering effect. The “octave” of eight magnitude-altering sets of indigs in turn disclose primary dichotomy into four positively altering and four negatively altering magnitude operators, with each set arranged in absolute arithmetical sequence of from one to four only.

1222.11

Indig congruences demonstrate that nine is zero and that number system is inherently octave and corresponds to the four positive and four negative octants of the two polar domains (obverse and reverse) of the octahedron__and of all systems__which systematic polyhedral octantation limits also govern the eight 45-degree-angle constituent limits of 360-degree unity in the trigonometric function calculations.

1222.12

The inherent + 4, - 4, 0, + 4, -4, 0 → of number also corresponds (a) to the four varisized spheres integrating tritangentially to form the tetrahedron (see Sec. 1222.20 and (b) to the octantation of the Coupler (see Sec. 954.20) by its eight allspace- filling Mites (AAB Modules) which, being inherently plus-or-minus biased, though superficially invariant (i.e., are conformationally identical); altogether provide lucidly synergetic integration (at a kindergarten-comprehendible level) of cosmically basic number behavior, quantum mechanics, synergetics, nuclear physics, wave phenomena in general, and topologically rational accountability of experience in general.

1222.20 Cosmically Absolute Numbers

There are apparently no cosmically absolute numbers other than 1, 2, 3, and 4. This primitive foumess identifies exactly with one quantum of energy and with the foumess of the tetrahedron’s primitive structuring as constituting the “prime structural system of Universe,” i.e., as the minimum omnitriangulated differentiator of Universe into insideness and outsideness, which alone, of all macro-micro Universe differentiators, pulsates inside-outingly and vice verse as instigated by only one force vector impinging upon it. (See Sec. 624.)

1222.30 Casting Out Nines

We can use any congruence we like, and the pattern will be the same. The wave phenomenon, increasing by four and decreasing by four, is an octave beginning and ending at zero. From this I saw that nine is zero.

1222.31

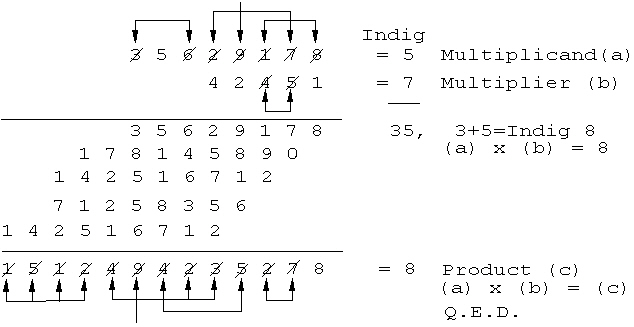
When I worked for Armour and Company before World War I, I had to add and multiply enormous columns of figures every day. As yet, neither commercially available adding machines nor electric calculators existed. The auditors showed us how to check our multiplications by “casting out nines.” This is done by inspecting all the input integers of multiplication, first crossing out any nines and then crossing out any combinations of integers that add to nine, exclusively within either the (a) multiplicands, (b) multipliers, or (c) products of multiplication, taken separately. This means we do not take combinations of integers occurring in other than their own respective (a), (b), or (c) sets of integers that add up to nine.

$$\begin{array}{r}\text{(a) Multiplier}\\ \times \text{ (b) Multiplicand}\\ \text{(c) Product}\end{array}$$

Cross out all nines, or any set of integers adding to nine, in any one of either the multiplier (a), the multiplicand (b), or the product (c).

1223.00 Wave Pulsation of Indigs

1223.10 Pulsative Octave

The interaction of all numbers other than nine creates the wave phenomenon described, i.e., the self-invertible, self-inside-outable octave increasing and decreasing pulsatively, fourfoldedly, and tetrahedrally. No matter how complex a number-aggregating sequence of events and conditions may be, this same number behavior phenomenon is all that ever happens. There is thus a primitively comprehensive, isotropically distributive, carrier-wave order omniaccommodatively permeating and embracing all phenomena. (See Sec. 1012.10)

1223.11

As the nine columns of Indig Table 2 show, I have integrated the digits of all the different multiplication systems and have always found the positively-negatively pulsative, octave, zero-nine-intervaled, ergo interference-free, carrier-wave pattern to be permeating all of them in four alternative interger-mix sequences; with again, four positively ordered and four negatively ordered sequence sets, all octavely ventilated by zero nines cyclically, ergo inherently, ergo eternally synchronized to non-inter- interferences.

1223.12

As will also be seen in Indig Table 2, the integer carrier waves can pulse in single sets, as in Columns 1 and 8; in double pairs, as in Columns 4 and 5; in triple triplets, as in Columns 3 and 6; and in double quadruplets, as in Columns 2 and 7__always octavely interspersed with zeros and, in the case of Columns 3 and 6, interspersed with zeros triangularly as well as octavely. This also means that the omnidirectional wave interpermutatings are accommodated as points or as lines; or as triangular areas; or as tetrahedral volumes__both positive and negative.

1223.13

Thus we are informed that the carrier waves and their internal-external zero intervalling are congruent with the omnitriangulated, tetraplaned, four-dimensional vector equilibria and the omniregenerative isotropic matrix whose univectorings accommodate any wavelength or frequency multiplying in respect to any convergently-divergently nuclear system loci of Universe.

1223.14

Not only is there an external zero intervalling between all the unique octave- patterning sets in every one of the four positive, four negative systems manifest, but we find also the wave-intermodulating indigs within each octave always integrating sum- totally internally to the octaves themselves as nines, which is again an internal zero content__this produces in effect a positive zero function vs. a negative zero function, i.e., an inside-out and outside-out zero as the ultracosmic zero-wave pulsativeness.²

(Footnote 2: See Sec. 1012, which describes a closest-sphere-packing model of the same phenomenon. If we make an X configuration with one ball in the center common to both triangles of the X, the ball at the intersection common to both represents the zero__or the place where the waves can pass through each other. The zero always accomodates when two waves come together. We know that atoms close-pack in this manner, and we know how wave phenomena such as radio waves behave. And now we have a model to explain how they do not interfere.)

1223.15

Thus we discover the modus operandi by which radio waves and other waves pass uninterferingly through seeming solids, which are themselves only wave complexes. The lack of interference is explained by the crossing of the high-frequency waves through the much lower-frequency waves at the noninterfering zero points, or indeed by the varifrequencied waves through both one another’s internal and external zero intervals. (See Illus. 1012.13A and B.)

1223.16

If the readers would like to do some of their own indig exploration they may be instructively intrigued by taking a book of mathematical tables and turning to the table of second powers of integers. If they undertake to indig each of those successively listed second-power numbers they will discover that, for the first 100 numbers listed, a unique sequence of 24 integers will appear that peaks at 25, reverses itself, and bottoms at one, only to turn again and peak at 50, bottom at 75, and peak again at the 100th number which, when analyzed, manifests a 2 × 2 × 2 = 8 = 23 × 3 = 24 four-dimensional wave. This four-dimensional wave is only comprehendible when we discover (see Sec. 982.62) the three-frequency reality of F3 × 2 l/2, 3, 4, 5, 6, the a priori, initially-volumed, ergo three-dimensional reality multiplied by the third power of omnidirectional growth rate.

1224.00 Wave Pulsation of Number 24

1224.10 Vector Equilibrium and Octave Wave

1224.11

The second powering of numbers apparently involves a 24-positive and 24- negative resonance phasing. The potential variables of the indigs of the second-powering of the 24 successive integers running between 0 and 25, and indigs of the 24 integers descending successively between 25 and 50, and repeating the 24 integers between 50 and 75, and the 24 integers between 75 and 100 ad infinitum, apparently account for all the equilibrious-disequilibrious, radiational-gravitational, convergent-divergent, curviwavilinear behaviors in respect to the vector equilibrium as well as for the unique rates of growth or contraction of closest-packed-spherical agglomerating.

1224.12

In respect to the progressive series of n2 product numbers as expressed in congruence-in-modulo- 10, a unique 24-integer series of terminal, submodulus-10, excess integers completes its series direction with 24 and makes its verse-and-reverse series at the common hinges of 252, 752, 1002 in increments of +24, -24, +24, -24, or in a positively occurring, three-octave-wave increment sequence followed each time by a reversely occurring, three-octave-wave, unique harmonic theme.

1224.13

The three-octave, 24-integer series is manifest in the convergent-divergent, tetrahedral wave propagations of the vector equilibrium wherein the eight tetrahedra share their nuclear sphere and then share their common apex spheres as they embrace that nuclear sphere by expanding in successive triangular closest-packed sphere layers. (Compare Secs. 1012.11 and 1033.030.)

1224.14

The lines omniinterconnecting the sphere centers of those successively embracing layers produce equiangular triangles, or electromagnetic fields, the sum of whose areas in each successive layer is always n2 of the number in each series in that layer. In contradistinction to the triangular field, in the series of triangularly closest-packed sphere layers, every two adjacent layers’ series produces the next greater n2 number of spheres, with the number of closest-packed sphere triangles in the waxing and waning phases of the series being governed by the frequency of the wave propagation elected for consideration in each instant.

1224.20 Recapitulation

1224.21 The interwave and intervolumetric behavior of the number 24 may be considered variously as follows:

• 24 A Quanta Modules per regular tetrahedron: (Tables 223.64 and 943.00; Secs. 910.11 and 942.10)
• 24 modules of regular tetrahedron as cosmic bridge between equilibrious prime number one of metaphysics and disequilibrious prime number one of physical reality (Sec. 954.51)
• B Quanta Modules per Coupler (asymmetric octahedron): (Table 223.64; Secs. 954.10, 954.21, and 954.46)
• 24 subparticle differentiabilities of the Coupler to provide for the 2, 3, 4, 6 combinations of proton-neutron intertransformabilities and isotopic variations: (Sec. 954.22)
• 24 positive and negative basic triangles (basic equilibrium 48 LCD triangles) defined by the 25 great circles of the vector equilibrium: (Secs. 453.01 and 1052.30)
• 24 total exterior vertexes of the vector equilibrium paired to produce 12 congruent, univalent external vertexes and to describe the eight tetrahedra, all of which share a common nuclear point to function in octavalent congruence as nuclear circuitry: (Secs. 1012.11 and 1033.030)
• 24 positively integrated vectors as the implosive, external, circumferentially embracing set of the four great circles of the vector equilibrium and the 24 negatively disintegrative, internal, radially explosive set, with both sets paired at the 12 vertexes: Secs. 450.11, 537.131, 615.06, 905.55, 955.02, 1011.40, and 1052.30)
• 24 interior and exterior A Quanta Modules of the isosceles dodecahedron: (Table 943.00)
• 24 A-and-B-Quanta-Module-volume of the nucleus-embracing cube formed by applying the eight Eighth-Octahedra to the eight triangular facets of the vector equilibrium: Secs. 905.44 and 982.62)
• 24 spherical right triangles of the spherical tetrahedron’s three-way great-circle grid: (Sec. 905.51)
• 24 highest common multiple of regular-tetrahedral-volume values of all congruently symmetric polyhedra of the hierarchy of concentric, symmetrical, rationally volumed geometries occurring within the isotropic vector matrix: (Sec. 982.70)
• 24 integer series of alternately convergent-divergent sequences with 24 unique terminal suffix excesses__in respect to the series of n2 numbers as expressed by congruence in modulo-10__which series peaks at 24 and commonly hinges at 25 to reverse descendingly again to hinge at 50 and then ascends to peak again to hinge at 75 and repeats, in this unique, three-octave, convergent-divergent, wave pulsating- propagating of harmonic themes mutingly inflected at the 25th hinge: (Sec. 1223.16)
• The 24 A or B Quanta Modules per 120 basic disequilibrium LCD triangles: (sec. 1053.36)
• The inherent subdivision of any tetrahedron, regular or irregular, into 24 equal modules: Sec. 961.44)
• The cosmic hierarchy limit of 24 active tetravolumes per each sphere-into-space and each space-into-sphere intertransforming of the complex of jitterbugs: (Sec. 1033.20)
• The 24 S Quanta Modules of the icosa-octa interrelationship within the four- frequency tetrahedron: (Sec. 988)
• The five sets of 24 each of the T or E Quanta Modules of the rhombic triacontahedron.

1224.30 Turnaround Terminals

1224.31

The powerful 24-ness number behavior with its great-circle congruences and three-octave harmonics may have significant ramifications embracing the unique frequencies of the chemical compoundings as well as the nuclear geometry elucidated elsewhere in this work. (Sec. 1033 passim.) The terminal-suffix excess integers of the series of second powers of numbers as expressed in congruence in modulo-10 displays the sequence of uniquely aberrating eccentricities in respect to the whole 24-integer phrases.

1224.32

The large figure “2”’ in the last column of the Indig Table (Fig. 1223.12B) shows that the terminal digits of the second powers of numbers turn around at the middling number 25.

1224.33

There are 24 positive and 24 negative unique numbers that reverse themselves between 0 and 50. This reflects three positive and three negative octaves with turnaround terminal zero accommodation.

1224.34

The “square” identifies that number of energy units occurring in the outer shell of all nuclear phenomena with the second-powering characteristic being that of both the gravitation and the radiational constant’s surface growth.