100.103

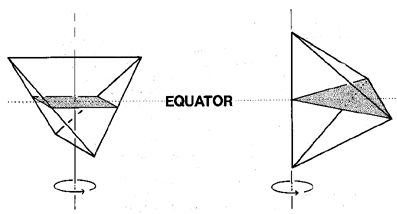
Fig. 100.103

Parallel and Perpendicular Halving of Tetrahedron:
Compare figures 527.08 (image) and 987.230B (image)

Link to original

Rational numerical and geometrical values derive from (a) parallel and (b) perpendicular halving of the tetrahedron. (See Fig. 100.103.) (a) The parallel method of tetrahedral bisecting has three axes of spin__ergo, three equators of halving. Parallel equatorial halving is both statically and dynamically symmetric. (b) The perpendicular method of tetrahedral bisecting has six axes of spin__ergo, six equators of halving. Perpendicular equatorial halving is only dynamically symmetric.