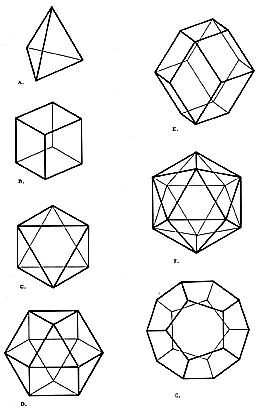
A. Tetrahedron: 4 faces, 4 vertexes, 6 edges. B. Cube: 6 faces, 8 vertexes, 12 edges. C. Octahedron: 8 faces, 6 vertexes, 12 edges. D. Vector Equilibrium (cuboctahedron): 14 faces, 12 vertexes, 24 edges. E. Rhombic dodecahedron: 12 faces, 14 vertexes, 24 edges. F. Icosahedron: 20 faces, 12 vertexes 30 edges. G. Pentagonal dodecahedron: 12 faces, 20 vertexes, 30 edges. Euler’s topological formula is f + (v - 2) = e, or f + v = e + 2. In any system, two vertexes may be considered polarized. These vertexes are then subtracted to balance the equation. This suggests the inherent twoness of Universe.