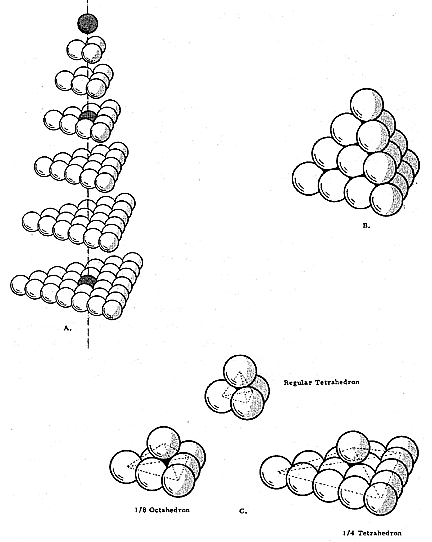
Fig. 415.55 Tetrahedral Closest Packing of Spheres: Nucleus and Nestable Configurations:
A. In any number of successive planar layers of tetrahedrally organized sphere packings, every third triangular layer has a sphere at its centroid (a nucleus). The 36-sphere tetrahedron with five spheres on an edge (four-frequency tetrahedron) is the lowest frequency tetrahedron system which has a central sphere or nucleus. B. The three-frequency tetrahedron is the highest frequency without a nucleus sphere. C. Basic “nestable” possibilities show how the regular tetrahedron, the 1/4-tetrahedron and the 1/8- octahedron may be defined with sets of closest packed spheres. Note that this “nesting” is only possible on triangular arrays which have no sphere at their respective centroids.